Assignment 4: Understanding mortgage calculations
Alright, I assume most of you haven't bought a house, so here's how mortgages works. To those of you that read my email, I'm sorry I didn't include the calculations, here they are.
So let's say I want to buy a $350,000 house, but I only have $50,000 saved up. That means I need a mortgage for $300,000. This is my principal.
The bank needs to make money, so they add on an interest rate. This interest rate is what confuses most people.
Example calculations for your assignment
Let's say the bank offered us a $300,000 mortgage, with 4.5% annual interest. Interest is compounded semi-annually (standard in Canada), and payments are made monthly.
P = principal = 300000
n = total number of payments = 5 years * 12 months/year = 60 payments
i = [r/c + 1]c/f - 1
r = annual interest rate = 4.5% = 4.5/100 = 0.045
c = compounding frequency per year = semi-annually = 2 per year
f = frequency of payments per year = monthly = 12 per year
i = [0.045/2 + 1]2/12 -1
i = [1.0225]1/6 -1
i = [1.003715] - 1
i = 0.003715
B = (P *i ) / (1 - (i + 1)-n
B = (300000 * 0.003715) / (1 - (0.003715 + 1)-60
B = 1114.5 / (1 - (1.003715)-60)
B = 1114.5 / (1 - 0.8005254)
B = 1114.5 / 0.19947
B = 5587.18
Your blended payment (ie. principal + interest) is $5,587.18
Your total interest+principal is your blended payment multiplied by the number of payments n : $5,587.18 x 60 = $335,230.80
Your total interest paid is $335,230.80 - $300,000 = $35,230.80
The interest/principal ratio is $35,230.80/$300,000 = 0.1174
The average interest paid per year is $35,230.80 / 5 years = $7,046.16
The average interest paid per month is $35,230.80 / 60 months = $587.18
The amortization expressed in years is 5 years.
Checking your results using TD Bank's mortgage calculator
TD Bank's Mortgage Payment Calculator
For Interest Rate, select "Enter your own Rate", then choose one of the CLOSED terms.

Bonus
If the user can select monthly, bi-weekly, or weekly payments, you just have to change n and f in your calculations to match the new number and frequency of payments.
If the compounding frequency changes, you have to change c in your calculations.
The last part is a little more difficult, but I hope most of you attempt it for the extra credit. Click on the "Amortization Schedule" in TD Bank's calculator to see how it works.
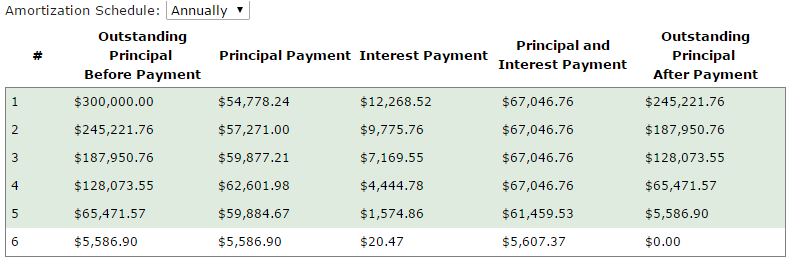
For the bonus, you need to show the following:
- blended payment amount (principal and interest payment)
- interest component (interest payment)
- principal component (principal payment)
- new balance owing (outstanding principal after payment)
Your blended payment doesn't change, but you can see how your principal/interest payments are changing. In the first year, we paid $54,778.24 to the principal, so we are left with $245,221.76 outstanding in the principal. For our second year, the new principal is now $245.221.76, instead of $300,000. That means the interest calculated on the new outstanding principal is going to be lower than in the first year. However, because my blended payment doesn't change, the amount that goes towards my principal payment increases. Line 5 and 6 are different, because Line 6 is actually your final payment, and Line 5 is one year's payments minus the final payment from Line 6.
